
Cette page provient de Documentation française de Blender 3D
http://blender.doc.fr.free.fr/lecture_ouverte
| <= Page précédante <= | Sommaire | => Page suivante => |
Chapitre 7. Courbes et surfaces
Les courbes et les surfaces sont des objets comme les maillages, mais ils diffèrents du fait qu'ils sont exprimés en termes de fonctions mathématiques, plutôt que comme une suite de points.
Blender met en application des courbes et des surfaces de Bézier et des Non Uniform Rational B-Splines (NURBS). Les deux, en suivant, cependant des lois mathématiques différentes, sont définies en termes d'ensemble de "sommets de contrôle" qui définissent un "polygone de contrôle". La manière dont la courbe et la surface sont interpolées (Bézier) ou attirées (NURBS) par ces derniers pourrait sembler identique, à première vue, aux surfaces de subdivision Catmull-Clark.
Comparées aux maillages, les courbes et les surfaces ont des avantages et des inconvénients. Puisque les courbes sont définies par moins de données, elles produisent de beaux résultats en utilisant moins de mémoire pendant le modelage, tandis que cela augmente pendant le rendu.
Certaines techniques de modelage, telle que l'extrusion d'un profil selon un chemin donné, ne sont possibles qu'avec des courbes. Mais le contrôle très fin sur chaque sommet du maillage, n'est pas possible avec des courbes.
Parfois les courbes et les surfaces sont plus avantageuses que les maillages, parfois les maillages sont plus utiles. Si vous avez lu le chapitre précédent, et si vous lisez celui-ci vous pourrez choisir d'utiliser les maillages ou les courbes.
7.1. Courbes
Valable à partir de Blender v2.31
Cette section décrit les courbes de Bézier et les NURBS, et en montre un exemple pratique.
7.1.1. Béziers
Les courbes de Bézier sont le type le plus généralement utilisé pour concevoir des lettres ou des logos. Elles sont également largement répandues dans l'animation, comme chemins pour que les objets se déplacent dessus et comme courbes IPO pour changer les propriétés des objets en fonction du temps.
Un point de contrôle (sommet) d'une courbe de Bézier est constitué d'un point et de deux poignées. Le point, au milieu, est utilisé pour déplacer le point de contrôle entier; le sélectionner sélectionne aussi les deux autres poignées, et vous permet de déplacer le sommet entier. Sélectionner une ou deux des autres poignées vous permet de modifier la forme de la courbe en les déplaçant.
Une courbe de Bézier est tangente au segment qui va du point à la poignée. La "raideur" de la courbe est contrôlée par la longueur de la poignée.
Il y a quatre types de poignées (Figure 7-1) :
- Poignée libre (en noir). Elles peuvent être utilisées de quelque façon que vous voulez. Raccourci : HKEY (permute entre Libre et Alignée) ;
- Poignée alignée (pourpre). Ces poignées se situent toujours sur une ligne droite. Raccourci : HKEY (permute entre Libre et Alignée) ;
- Poignée vecteur (en vert). Les deux poignées se dirigent toujours vers la poignée précédente ou la poignée suivante. Raccourci : VKEY ;
- Poignée automatique (jaune). Cette poignée a une longueur et une direction complètement automatiques, réglées par Blender pour assurer le résultat le plus lisse. Raccourci : SHIFT-H.
Figure 7-1. Types de poignées pour les courbes de Béziers.

Les poignées peuvent être déplacées, subir une rotation et mises à l'échelle exactement comme un sommet ordinaire de maillage.
Dés que les poignées sont déplacées, le type est modifié automatiquement :
- Poignée Automatique devient Alignée ;
- Poignée Vecteur devient Libre ;
Bien que la courbe de Bézier soit un objet mathématique continu elle doit néanmoins être représentée sous forme "discontinue" d'un point de vue de rendu.
Ceci peut être fait en réglant une propriété de résolution, qui définit le nombre de points qui sont calculés entre chaque paire de points de contrôle. Une résolution différente peut être réglée pour chaque courbe de Bézier (le schéma 7-2).
Figure 7-2. Réglage de la résolution Bézier

7.1.2. NURBS
Les courbes NURBS sont définies comme polynômes rationnels, et sont plus courantes, à proprement parler, que les B-Splines conventionnelles et que les courbes de Bézier, d'autant qu'elles peuvent suivre exactement n'importe quel profil. Par exemple, un cercle de Bézier est l'"approximation" polynomiale d'un cercle, et cette approximation est apparente, tandis qu'un cercle NURBS est "exactement" un cercle. Les courbes NURBS ont un grand ensemble de variables, qui vous permettent de créer des formes mathématiquement pures (Figure 7-3). Cependant, travailler avec elles exige un peu plus de théorie :
Figure 7-3. Boutons de contrôle des Nurbs.

- Knots (Noeuds). Les courbes Nurbs disposent d'un knot vector (un vecteur nodal), une rangée de nombres qui spécifie la définition paramétrique de la courbe. Deux pré-réglages sont importants pour cela. Uniform (Uniforme) produit une division uniforme pour les courbes fermées, mais utilisé avec des formes ouvertes produira des extrémités "libres", qui sont difficiles à localiser précisément. Endpoint (Extrémité) régle les noeuds de façon à ce que les premiers et les derniers sommets fassent toujours partie de la courbe, ce qui les rend plus faciles à positionner.
- Order (Ordre). L'order est la 'profondeur' du calcul de la courbe. Order '1' est un point, Order '2' est linéaire, Order '3' est quadratique, et ainsi de suite. Utilisez toujours Order '5' pour les profils courbes parce qu'il se comporte avec fluidité en toutes circonstances, sans produire de discontinuités irritantes dans le mouvement. En terme mathématique, ceci est l'ordre du numérateur et du dénominateur du polynôme rationnel définissant la NURBS.
- Weight (poids). Les courbes Nurbs ont un 'poids' par sommet, le degré auquel un sommet participe à la traction de la courbe.
Figure 7-4. Réglage du Polygone de contrôle et du poids de la NURBS.

La figure 7-4 montre le réglage du vecteur Nodal et l'effet que produit la variation de poids d'un noeud. Comme avec les Béziers, la résolution peut être établie sur la base d'une seule courbe.
7.1.3. Exemple pratique
Les outils de courbes de Blender fournissent une manière rapide et facile d'établir de beaux textes et logos extrudés. Nous allons utiliser ces outils pour transformer le croquis approximatif d'un logo en objet 3D fini.
La Figure 7-5 montre le dessin du logo que nous allons élaborer.
Figure 7-5. L'esquisse du logo.

Tout d'abord, nous allons importer notre croquis original pour l'utiliser comme modèle. Blender supporte les formats d'images TGA, PNG et JPG. Pour charger l'image, sélectionnez View >>Background Image (Vue de l'image d'arrière plan) dans le menu de la fenêtre 3D que vous utilisez. Un panneau transparent va apparaître, vous permettant de sélectionner une image à utiliser comme arrière plan. Activez le bouton BackGroundPic (Image d'arrière plan) et utilisez le bouton LOAD (Charger) pour localiser l'image que vous voulez utiliser comme modèle (Figure 7-6). Vous pouvez régler la "puissance" de l'image d'arrière plan avec le bouton à glissière Blend (Opacité).
Figure 7-6. Réglages de la fenêtre 3D.

Débarrassez-vous du panneau avec ESC ou en appuyant sur le bouton X dans l'en-tête du panneau (Figure 7-7). Quand vous avez fini, vous pouvez cacher l'image d'arrière plan en retournant au panneau et en désélectionnant le bouton BackGroundPic.
Figure 7-7. L'esquisse du logo chargée en arrière plan.

Ajoutez une nouvelle courbe en pressant SPACE>>Curve>>Bezier Curve. Un segment courbé va apparaître et Blender va se mettre en mode édition. Nous allons déplacer et ajouter des points pour faire une forme fermée qui décrit le logo que vous essayez de tracer.
Vous pouvez ajouter des points à la courbe en sélectionnant une des deux extrémités, puis en maintenant CTRL et en cliquant LMB. Notez que le nouveau point va être connecté au point précédemment sélectionné. Une fois que le point a été ajouté, il peut être déplacé en sélectionnant le sommet de contrôle et en pressant GKEY. Vous pouvez changer l'angle de la courbe en déplaçant les poignées associées à chaque sommet. (Figure 7-8).
Figure 7-8. Poignées de Bézier.

Vous pouvez ajouter un nouveau point entre les deux points existants en les sélectionnant et en appuyant sur WKEY>>Subdivide (Subdiviser) (Figure 7-9).
Figure 7-9. Ajouter un point de contrôle.

Les points peuvent être supprimés en les sélectionnant et en pressant XKEY>>Selected (Sélectionné). Pour couper une courbe en deux, sélectionnez deux sommets de contrôle adjacents et appuyez sur XKEY>>Segment.
Pour faire un sommet pointu, sélectionnez un sommet de contrôle et appuyez sur VKEY. Vous remarquerez que la couleur des poignées change de violet à vert (Figure 7-10). A ce point, vous pouvez déplacer les poignées pour ajuster le dessin de la courbe et quitter le sommet de contrôle (Figure 7-11).
Figure 7-10. Poignées de Vecteur (en vert).
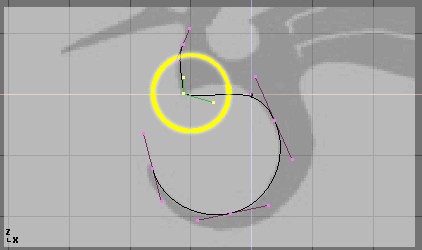
Figure 7-11. Poignées Libres (en noir).

Pour fermer la courbe et la transformer en simple boucle continue, sélectionnez au moins un des points de contrôle sur la courbe et appuyez sur CKEY. Ceci reliera le dernier point de la courbe au premier (Figure 7-12). Vous devrez peut-être ajouter et manipuler des poignées supplémentaires pour obtenir la forme que vous voulez.
Figure 7-12. Le contour fini

Quitter le mode édition avec TAB et entrer en mode ombré avec ZKEY devrait révéler que la courbe génère un rendu "de forme solide" (Figure 7-13). Nous voulons découper quelques ouvertures dans cette configuration pour représenter les yeux et des détails dans l'aile du dragon.
Astuce : Surfaces et ouvertures En travaillant avec des courbes, Blender détecte automatiquement les ouvertures dans la surface et les manipule en conséquence avec les règles suivantes. Une courbe fermée est toujours considérée comme la limite d'une surface et par conséquent rendue comme surface plane. Si une courbe fermée est totalement incluse dans une autre, la première est soustraite de la dernière, définissant efficacement une ouverture. |
Figure 7-13. Le logo ombré.

Retournez ou mode filaire avec ZKEY et entrez à nouveau en mode édition avec TAB. Toujours en mode édition, ajoutez une courbe 'cercle' avec SPACE>>Curve>>Bezier Circle (ESPACE>> Courbe>>cercle Bezier) (Figure 7-14). Réduisez l'échelle du cercle à une taille appropriée avec SKEY et déplacez le avec GKEY.
Figure 7-14. Ajout d'un cercle.
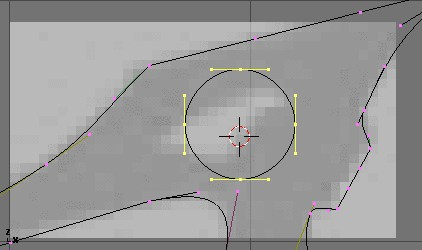
Formez le cercle en utilisant les techniques que nous avons apprises (Figure 7-15). Rappelez-vous d'ajouter des sommets au cercle avec WKEY>>Subdivide (Subdiviser).
Figure 7-15- Définition de l'oeil.

Créez la découpe de l'aile en ajoutant un cercle de Bézier, en convertissant tous les points en angles aigus, puis en les ajustant si besoin est. Vous pouvez dupliquer ce contour pour créer la deuxième découpe plus rapidement. Pour cela, assurez-vous qu'aucun point n'est sélectionné, puis déplacez le curseur sur un des sommets de la première découpe et sélectionnez tous les points liés avec LKEY (Figure 7-16). Dupliquez la sélection avec SHIFT-D et déplacez les nouveaux points à la bonne position.
Figure 7-16. Définition de l'aile.

Pour ajouter d'autres géométries qui ne sont pas reliées au corps principal (en plaçant un "orbe" (espace circulaire orbital) dans la queue incurvée du dragon par exemple), employez le menu SHIFT-A pour ajouter d'autres courbes comme représenté sur la Figure 7-17.
Figure 7-17. Placement d'un corps rond dans la queue.

Maintenant que nous avons la courbe, nous devons régler ses options d'épaisseur et de biseau. La courbe étant sélectionnée, allez à EditButtons (Boutons d'édition) (F9) et localisez le panneau Curves and Surface (Courbes et surfaces). Le paramètre Ext1 règle l'épaisseur de l'extrusion tandis que Ext2 règle la taille du biseau. BevResol définit la manière dont se présentera le biseau, pointu ou arrondi.
La Figure 7-18 montre le réglage utilisé pour extruder cette courbe.
Figure 7-18. Réglage du biseau.

Astuce : Passer des Courbes aux Maillages Pour effectuer des opérations de modelage plus complexes, convertir la courbe en maillage avec ALT-C>>Mesh (Maillage). Notez que c'est une opération à sens unique: vous ne pouvez pas convertir un maillage en courbe. |
Figure 7-19. Rendu final.

| <= Page précédante <= | Sommaire | => Page suivante => |
Url de la page :
http://blender.doc.fr.free.fr/lecture_ouverte/index.php?page=89